Amidation is one of the most common post-translational modification in which the C-terminal carboxyl group is replaced by an amide group1–5. Amidation plays an important role in peptidesand peptide hormones. More than half of all mammalian peptide hormones and more than 80 % of all insect hormones have amidated C-termini1. The mechanism of amidation is different depending on whether the modification takes place in vivo or in vitro. Amidation makes a peptide less susceptible to proteolytic degradation, which increases its half-life in the bloodstream2. By replacing the ionizable carboxyl group at the C-terminus with a nonionizable amide group,the physicochemical properties of the peptide can be altered. One example would be increased hydrophobicity under physiological conditions, which is essential for bioactive peptides involved in receptor recognition and signal transduction2–4. In addition, amidation influences the binding affinity of the peptides to their G-protein coupled receptors2,4.
Amidation (in vivo)
Overview
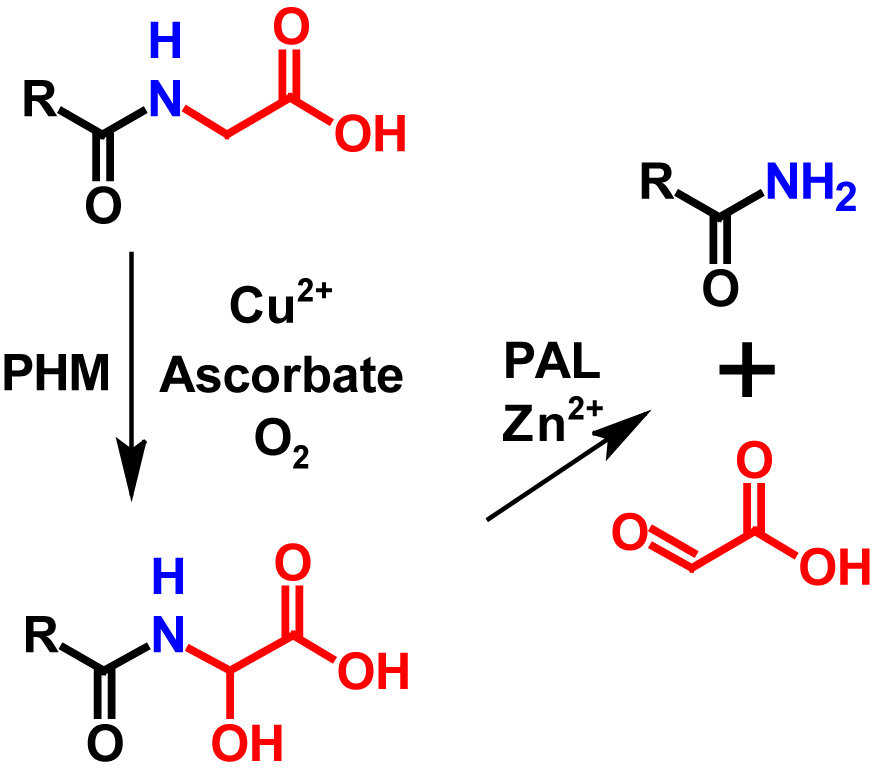
Amidation in vivo is a common post-translational modification in peptides and peptide hormonesin which the N-Cα bond of a C-terminal glycine is cleaved in two steps by the bifunctional enzyme peptidylglycine-α-amidating monooxygenase (PAM), resulting in an amidated C-terminus.
| pKa | NC | Loss | Gain | Deltamass | H | AA | UV-Spec | Pattern |
| – | No | C2H3O2 | H | Av: -58.0362 M: -58.0055 | – 3 | $ | – | (?<=G)$ |
In-depth mechanism
Amidation in vivo is one of the last modifications in peptide maturation and occurs in the trans-Golgi network or in secretory vesicles2. It is not simply the result of a transamination reaction, but is performed by the bifunctional enzyme peptidylglycine-α-amidating monooxygenase (PAM), which catalyses the reaction in two steps1–3,5. PAM is an integral membrane proteine that specifically recognizes C-terminal glycines and amidates them. PAM has two enzymatic domains inside the secretory pathway lumen and a small C-terminal domain in the cytosol. The catalytic domain involved in the first step is called peptidylglycine α-hydroxylating monooxygenase (PHM). PHM uses peptidylglycine as substrate and converts it into an α-hydroxyglycine intermediate. The presence of copper, ascorbate as well as molecular oxygen is required for this reaction to occur. The second catalytic domain is called peptidyl-α-hydroxyglycine α-amidating lyase (PAL). PAL is a zinc dependent enzyme which converts the α-hydroxyglycine intermediate into an amidated peptide by cleaving the N-Cα bond and simultaneously releases glyoxylate1,2. The amidated peptide shows a mass loss of 58 Da compared to its precursor5. Additionally, in RPLC since the carboxyl group is protonated and thus more hydrophobic than the amide group, the hydrophobicity of the protein is lowered by 3 (+ 1 glycine clipping / – 4 amidation). The mechanism of amidation in vivo is shown in figure 1.
Amidation (in vitro)
Overview
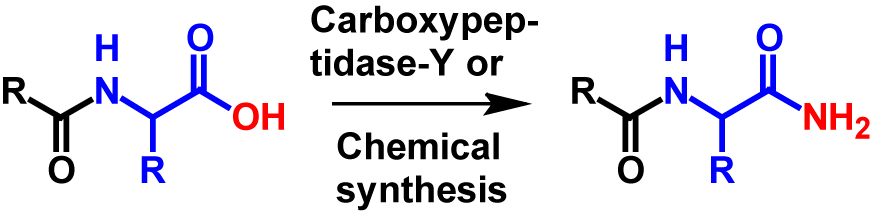
Amidation in vitro is an artificial modification that can be introduced at the C-terminus of a protein whereby the carboxyl group is replaced by an amide group. The C-terminal amide can be formed by chemical synthesis or by catalysation of carboxypeptidase-Y.
| pKa | NC | Loss | Gain | Deltamass | H | AA | UV-Spec | Pattern |
| – | No | OH | NH2 | Av: -0.9848 M: -0.9840 | – 4 | $ | – | – |
In-depth mechanism
Much research has been carried out to develop a more efficient amidation reaction, in particular due to its industrial application in the production of peptid amides for therapeutic purposes. Therefore, several methods have been developed. Four methods in particular have proved successful. These four methods include amidation by an α-amidating enzyme from a natural source, amidation by a recombinant α-amidating enzyme, enzymatic transacylation by carboxypeptidase-Y and chemical synthesis1. For the latter two methods, it is not necessary that a glycine is present at the C-terminus. The carboxyl group is directly exchanged for an amide group without partially cleaving off the C-terminal glycine. Therefore, with these two methods only a mass loss of 1 Da occurs compared to its precursor3,4. Also, the hydrophobicity in RPLC is reduced by 4 because the partial clipping of the C-terminal glycine is no longer carried out. The mechanism for amidation of the C-terminus by carboxypeptidase-Y and chemical synthesis is shown in figure 2.
References
- 1.Kim K-H, Seong BL. Peptide amidation: Production of peptide hormonesin vivo andin vitro. Biotechnology and Bioprocess Engineering. 2001;6:244–251. doi:10.1007/BF02931985
- 2.Kumar D, Eipper BA, Mains REBT-RM in BS. Amidation☆. In: Reference Module in Biomedical Sciences. Elsevier; 2014:1–5. doi:https://doi.org/10.1016/B978-0-12-801238-3.04040-X
- 3.Cui W, Niu S, Zheng L, et al. Prediction of protein amidation sites by feature selection and analysis. Molecular Genetics and Genomics. 2013;288:391–400. doi:10.1007/s00438-013-0760-x
- 4.Marino G, Eckhard U, Overall CM. Protein Termini and Their Modifications Revealed by Positional Proteomics. ACS Chemical Biology. 2015;10:1754–1764. doi:10.1021/acschembio.5b00189
- 5.An Z, Chen Y, Koomen JM, Merkler DJ. A mass spectrometry-based method to screen for ɑ-amidated peptides. Proteomics. 2012;12:173–182. doi:10.1002/pmic.201100327
Jon Grolimund’s article on amidation provides a comprehensive overview of this crucial post-translational modification, highlighting its significance in peptide biology. Amidation, particularly at the C-terminus, is essential for the stability and functionality of many peptide hormones, as it enhances their resistance to proteolytic degradation and increases their half-life in circulation. The detailed explanation of the enzymatic processes involved, particularly the role of peptidylglycine-α-amidating monooxygenase (PAM), is particularly enlightening. It’s fascinating how amidation alters the physicochemical properties of peptides, such as increasing hydrophobicity, which is vital for receptor interactions and signal transduction. The distinction between in vivo and in vitro amidation… Read more »